φ: la sezione aurea
Introduzione
La sezione aurea, in matematica e in arte, è una proporzione geometrica basata su di un rapporto specifico.
La parte maggiore sta alla minore come l’intera sta alla parte maggiore.
a:b=b:(a-b)
Es:
2:1=1:1 NO
1.6:1=1:0.6 SI
Rettangolo aureo
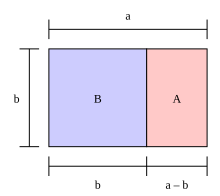
Il rettangolo aureo è un rettangolo le cui proporzioni sono basate sulla proporzione aurea. Ciò significa che il rapporto fra il lato maggiore e quello minore, a : b, è identico a quello fra il lato minore e il segmento ottenuto sottraendo quest'ultimo dal lato maggiore b : a-b (il che implica che entrambi i rapporti siano φ = 1,618).
Spirale aurea
In geometria, la spirale aurea è una spirale logaritmica con fattore di accrescimenti b di crescita pari a φ, la sezione aurea.
ƒrattali
Introduzione
Nelle misurazione è chiaro che più il passo p, ovvero la modalità di misura, è piccolo, maggiore sarà la precisione L. Un uomo può misurare la lunghezza nell'ordine di grandezza del metro, ma il fisico prosegue misurando in scala atomica; il matematico non ha limiti, il passo p e la precisione L sono tendenti all'inifinito.
La costa italiana
Pensiamo di misurare la costa italiana: potremo approssimare a circa il perimetro del rettangolo avente per dimensioni la distanza Aosta-Agrigento e la distanza Rimini-Genova, ottenendo una misura relativamente corretta. Oppure possiamo fotografare dall'altro tutta la penisola e, in scala, misurare attraverso le foto. Misura più corretta ma non ancora di buona approssimazione. Pensiamo di prendere un palo di un metro e, posizionando un punto A, porre questo palo lungo la costa arrivando al punto B. Segnando il punto B, posizioniamo il palo in quel punto e proseguiamo al punto C, così facendo per tutta la costa. Otterremo una misura molto accurata. Potremo proseguire fino all'ordine dei cm, avendo pazienza, ma per un matematico si può continuare così all'infinito: iterazione.
Casi eccezionali
Quest'operazione, in linea pratica è possibile, ma vi sono casi reali di figure chiuse in cui diminuendo p, L aumenta di precisione senza arrivare mai alla perfezione. Queste linee sono quindi infinite anche se racchiudono uno spazio definito. Caso di frattale.
Curva di Koch
Chiaro esempio di queste tipologie di linee è la curva di Koch. Essa difatti tende ad avere una lunghezza pressoche infinita. La sua costruzione avviene di fatti con un iterazione:
- Si prenda un triangolo equilatero e si dividano i lati in tre segmenti congruenti.
- Sul segmento centrale si costruisca un altro triangolo equilatero
- Si riproceda con lo stesso procedimento per ogni nuovo triangolo equilatero ottenuto
Se indichiamo con a il lato del triangolo iniziale, il suo perimetro è 3a. Alla prima iterazione ciascun nuovo lato diviene 4⁄3a, cioè aumenta di 1⁄3a. Questo aumento si ripete per ogni iterazione, per cui troviamo una linea di lunghezza infinita che racchiude area definita.
Ora, ciascun “ricciolo” di questa curva è formato da infiniti riccioli più piccoli, per cui, con tutte quelle cuspidi, è impossibile misurarne la lunghezza, come facevamo con la A7. D’altra parte, usare due dimensioni per una linea appare sciocco: per questo, i matematici hanno ideato una definizione generalizzata di “dimensione”, legata alla copertura di una curva, in questo caso, con dei cerchi di raggio fissato. Riducendo il raggio dei cerchi, aumenta il numero di cerchi che servono per coprire la curva: per una retta, ad esempio, si avrà
e per un quadrato, allo stesso modo,
Vediamo che per una dimensione si ha che il numero di cerchi è inversamente proporzionale al raggio, mentre per due dimensioni è inversamente proporzionale al quadrato del raggio: per una qualunque figura si ha che n∝ra, dove a è la dimensione della figura. Nel caso della curva di Koch, si ha a = 1,2619, cioè ha più di una dimensione e meno di due.
La sua dimensione è frattale.
Omotetia Interna
La principale caratteristica di un oggetto frattale è l’autosomiglianza o autosimilitudine. Tale proprietà consiste nel fatto che la forma di un oggetto presenta le stesse caratteristiche globali qualunque sia la scala di Dalla geometria euclidea alla geometria frattale: un ipermedia per interpretare la Natura, l’Universo e l’Uomo stesso osservazione. Tale proprietà fu spiegata da Mandelbrot attraverso il concetto di omotetia interna, una forma più generale del concetto di omotetia già noto ai matematici, per cui un vettore nel piano tramite una omotetia viene trasformato in un altro vettore avente la stessa direzione, lo stesso verso, ma modulo moltiplicato per un fattore che prende nome di “rapporto di omotetia”.